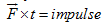Q.No.13.9: - What is Wheatstone bridge? How
it be used to determine an unknown resistance?
Ans: - Wheatstone bridge is used to determine unknown resistance of
a wire. The circuit is consists of four resistances R1, R2,
R3, R4 connected in such a way as to form a loop or mesh
ABCDA. A battery of emf E is connected between points A and C. A galvanometer
of resistance Rg is connected between the points B and D.
When the bridge is balanced, it
satisfied the following relation
R1/R2 = R3/R4
Or, R4
= R2.R3/R1
If the value of R1,
R2, and R3 are known then R4 can be
calculated. The galvanometer should not show any deflection by adjusting the
potential between terminals B and D. (Sorry for Diagram.
Pleas concert with Text Book for diagram.)